Абукус

Примечания

1. .
2. ↑ Депман И. Я. История Арифметики. — изд. «Просвещение», Москва, 1965, стр.81
3. , pp. 252–253
4. , p. 2
5. , p. 2
6. , p. 4
7. , p. 1
8. , p. 2
9. ↑ , p. 17
10. , p. 2
11. Учение Герберта об абаке тщательно изучил и прокомментировал в конце XIX — начале XX веков Н. М. Бубнов.
12. БСЭ, изд. 2, т. 31, стр. 568
13.  (англ.). Дата обращения: 9 декабря 2020.
14. Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд., испр. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
15. Глаголев Н. А. Глава II. Декартов абак для уравнений с тремя переменными (сетчатые номограммы) // Курс номографии. — М.: Высшая школа, 1961. — С. 23—60.

Преимущества использования

Использование древних счет – абакуса (соробан, суаньпань) легло в основу методики счёта – ментальная арифметика, которая направлена на всестороннее развитие ребёнка, помогает не только выполнять в уме операции с молниеносной скоростью, но раскрывает потенциал, заложенный природой.

Использование этого устройства на занятиях имеет ряд преимуществ перед счётом на калькуляторе или бумаге. Основное – это умение производить числовые операции в уме, без использования записей. Выполнение таким образом арифметических действий, предполагает работу двух рук, при этом активируются сразу оба полушария головного мозга.

Активация, как правого (образное мышление), так и левого (логическое мышление) полушария мозга, приводит к формированию нейронных связей между ними

Тем самым помогая улучшить память (как краткосрочную, так и долгосрочную), внимание, сформировать нестандартность мышления и тем самым уверенность в себе

Работа с костяшками влияет на мелкую моторику, что в свою очередь способствует общему развитию, в том числе и интеллектуальному. Косвенным образом происходит и развитие воображения, так как, переходя с абакуса на ментальный счет, необходимо представлять вычисления на нем, используя воображение.

Таким образом, счет на абакусе способствует всестороннемуинтеллектуальному развитию, а именно:

• Развитию умственных и творческих способностей;
• Формированию нейронных связей между левым и правым полушариями головного мозга;
• Развитию навыков сложных расчетов в уме и увеличению скорости обработки информации;
• Развитию внимания, памяти, мышления и воображения.

Как устроен абакус

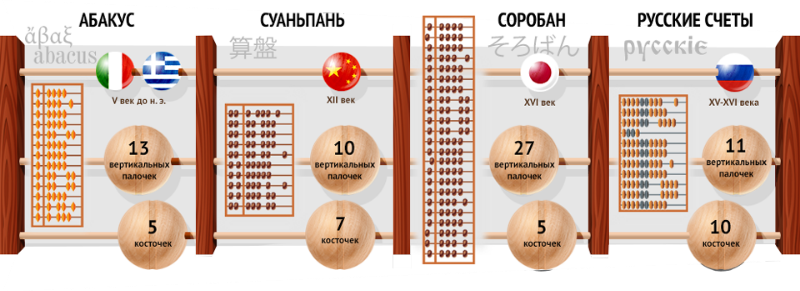
Ментальная арифметика и история её возникновения неразравно связаны с абакусом. Внешне счёты выглядят как прямоугольник с вертикальными спицами (их тринадцать, но бывает еще и усеченный абакус с меньшим количеством спиц), разделенный горизонтальной длинной перегородкой. В каждом ряду абакуса находится пять косточек: верхняя косточка — это цифра пять (как говорили японцы — «небесная косточка») и под перегородкой — четыре «земные» косточки, каждая из которых равна единице.

Когда дети только начинают изучать ментальную математику, тренеры обязательно рассказывают им историю возникновения методики и абакуса

Родителям и детям важно и интересно знать, почему этот простой, но очень эффективный инструмент устного счета помогает не только решать математические примеры, но и развивать уверенность в себе и навык многозадачности

Теперь решим уравнение

Умножение: 7 раз первое число, то есть 2, или 2 десятки. Это дает нам ответ 14 или 14 десятков, как показано на рисунке

Не очищайте 7.
Прежде чем продолжить, обратите внимание на ответ. Вы увидите, что первый продукт помещен рядом с 7

Этот результат был предсказан на основании способа постановки проблемы. Первое произведение находится в столбцах сотен, десятков и единиц. Нам еще нужно вычислить число 5.
Теперь умножьте: 7 раз 5. Это дает ответ 35 или 3 десятков и 5 единиц, которые можно добавить к 140. Ваш ответ будет: 175, как показано на фотографии. А теперь остановите счеты абакуса.

На счетах показан расчет «25 X 7».

Счеты, показывающие «9 х 50».

Деление

Проходить деление на абакусе нужно сразу после понимания и автоматизации умножения. Учебный процесс начните с пояснений принципов работы на счетах. Ребенок должен действовать так:

1. Мысленно разделить абакус на две половины по ширине. Это поля для знаменателя и ответа.

2. Цифру для деления выставить справа.
3. Слева будет ответ.
4. Писать итог деления нужно с крайнего столбца.

Посмотрите видео, в котором подробно объяснен принцип деления:

Продолжите изучать деление в этом ролике:

Делим 62 на 2

• Сначала отложим первое число (62) на абакусе.
• Делим десяток: 60 : 2 = 30.
• Откладываем в поле ответа 3 костяшки в крайнем ряду.
• Делим единицы: 2 : 2 = 1.
• Откладываем 1 костяшку в поле ответа в следующем ряду.
• Оцениваем итог. Получилось 31.

Делим 864 на 4

• Откладываем 864 на счетах.
• Оставляем в поле ответа не менее трех рядов свободными.
• Делим 800 на 4, получается 200.
• Поднимаем 2 костяшки в крайнем ряду для ответа.
• Делим 60 на 4. Получаем число с остатком. Придется умножить 4 на число меньше 6, но ближайшее к 4. Умножаем: 4 х 1, получается 4.
• Поднимаем 1 костяшку во втором ряду для ответа.
• Умножаем полученные 4 на 6 для восстановления равновесия чисел. Получается 24.
• Теперь делим 24 на 6. Ответ: 4.
• Поднимаем 4 костяшки в третьем ряду в поле ответов.
• Оцениваем результат – 216.

Литература

• Абакос // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Гутер Р. С., Полунов Ю. Л. От абака до компьютера. — 2-е изд., испр. и доп. — М.: Знание, 1981. — 240 с. — (Библиотека «Знание»). — 100 000 экз.
• Gaisford, Thomas. Etymologicon Magnum seu verius Lexicon Saepissime vocabulorum origines indagans ex pluribus lexicis scholiastis et grammaticis anonymi cuiusdam opera concinnatum (лат.). — Amsterdam, The Netherlands: Adolf M. Hakkert, 1962.
• Huehnergard, John (2011), Appendix of Semitic Roots, under the root ʾbq., American Heritage Dictionary of the English Language (5th ed.), Houghton Mifflin Harcourt Trade, ISBN 978-0-547-04101-8

Klein, Ernest (1966), abacus, A Comprehensive Etymological Dictionary of the English Language, vol. I: A-K, Amsterdam: Elsevier Publishing Company 

• Lasserre, Franciscus; Livadaras, Nicolaus. Etymologicum Magnum Genuinum: Symeonis Etymologicum: Una Cum Magna Grammatica (неопр.). — Rome, Italy: Edizioni dell’Ateneo, 1976. — Т. Primum: α — άμωσϒέπωϛ.
• Onions, C. T.; Friedrichsen, G. W. S. & Burchfield, R. W. (1967), abacus, The Oxford Dictionary of English Etymology, Oxford, UK: Oxford at the Clarendon Press

• Pullan, J. M. The History of the Abacus (неопр.). — New York, NY: Frederick A. Praeger, Inc., Publishers, 1968. — ISBN 978-0-09-089410-9.
• de Stefani, Aloysius. Etymologicum Gudianum quod vocatur; recensuit et apparatum criticum indicesque adiecit (неопр.). — Leipzig, Germany: Teubner, 1909. — Т. I.

Сложение и вычитание

В youtube большое количество видеоуроков по ментальной арифметике. Перед решением примеров на отработку формул, рекомендую изучить теорию

Также обучиться формулам бесплатно и набрать скорость в счете на абакусе можно при помощи приложения для Android Simple Soroban (в отличие от других аналогичных приложений в Simple Soroban можно одновременно перемещать несколько косточек, что очень важно в технике пальцев). Формулы для решения примеров на абакусе до 5 называют младшими товарищами, до 10 старшими товарищами, составные формулы микс формулами

Некоторые центры называют их друзьями, семьей и т. д. Суть не в названии. За 2000 лет формулы не изменились. Главное их понять и набрать скорость как при решении на счётах, так и в ментальном счете.

План обучения преподавателей:

— прямой счет на однозначных числах

— младшие товарищи

— старшие товарищи

— двузначные числа

— составные формулы

— переход на 50, 100

— трехзначные

— подготовка к умножению и делению, умножение и деление на абакусе.

Фундаментальные упражнения на отработку составных формул.

+6=-5+1+10

5+6, 6+6, 7+6, 8+6, 15+6, 16+6, 17+6, 18+6, 25+6, 26+6, 27+6, 28+6, 35+6, 36+6, 36+6, 37+6, 38+6

+7=-5+2+10

5+7, 6+7, 7+7, 15+7, 16+7, 17+7, 25+7, 26+7, 27+7, 35+7, 36+7, 37+7

+8=-5+3+10

5+8, 6+8, 15+8, 16+8, 25+8, 26+8, 35+8, 36+8

+9=-5+4+10

5+9, 15+9, 25+9, 35+9, 55+9, 65+9, 75+9, 85+9

— 6=-10+5—1

11–6, 12–6, 13–6, 14–6, 21–6, 22–6, 23–6, 24–6, 31–6, 32–6, 33–6, 34–6, 41–6, 42–6, 43–6, 44–6

— 7=-10+5—2

12–7, 13–7, 14–7, 22–7, 23–7, 24–7, 32–7, 33–7, 34–7, 42–7, 43–7, 44–7

— 8=-10+5—3

13–8, 14–8, 23–8, 24–8, 33–8, 34–8, 43–8, 44–8, 63–8, 64–8, 73–8, 74–8, 83–8, 84–8, 93–8, 94–8

— 9=-10+5—4

14–9, 24–9, 34–9, 44–9, 64–9, 74–9, 84–9, 94–9

Фундаментальные упражнения на отработку формул старших товарищей (минус) −9=-10+1

10–9, 11–9, 12–9, 13–9, 15–9, 16–9, 17–9, 18–9, 20–9, 21–9, 22–9, 23–9, 25–9, 26–9, 27–9, 28–9

— 8=-10+2

10–8, 11–8, 12–8, 20–8, 21–8, 22–8, 30–8, 31–8, 32–8, 40–8, 41–8, 42–8

— 7=-10+3

10–7, 11–7, 20–7, 21–7, 30–7, 31–7, 40–7, 41–7, 60–7, 61–7, 70–7, 71–7, 80–7, 81–7, 90–7, 91–7

— 6=-10+4

10–6, 15–6, 20–6, 25–6, 30–6, 35–6, 40–6, 45–6, 60–6, 65–6, 70–6, 75–6, 80–6, 85–6, 90–6, 95–6

— 5=-10+5

10–5, 11–5, 12–5, 13–5, 14–5, 20–5, 21–5, 22–5, 23–5, 24–5, 30–5, 31–5, 32–5, 33–5, 34–5, 41–5, 42–5,

43–5, 44–5

— 4=-10+6

10–4, 11–4, 12–4, 13–4, 20–4, 21–4, 22–4, 23–4, 30–4, 31–4, 32–4, 33–4, 40–4, 41–4, 42–4, 43–4

— 3=-10+7

10–3, 11–3, 12–3, 20–3, 21–3, 22–3, 30–3, 31–3, 32–3, 40–3, 41–3, 42–3

— 2=-10+8

10–2, 11–2, 20–2, 21–2, 30–2, 31–2, 40–2, 41–2, 60–2, 61–2

— 1=-10+9

10–1, 20–1, 30–1, 40–1, 60–1, 70–1, 80–1, 90–1

Переход через 50

+50

41+9

42+9 42+8

43+9 43+8 43+7

44+9 44+8 44+7 44+6

45+9 45+8 45+7 45+6 45+5

46+9 46+8 46+7 46+6 46+5 46+4

47+9 47+8 47+7 47+6 47+5 47+4 47+3

48+9 48+8 48+7 48+6 48+5 48+4 48+3 48+2

49+9 49+8 49+7 49+6 49+5 49+4 49+3 49+2 49+1

— 50

50–9 50–8 50–7 50–6 50–5 50–4 50–3 50–2 50–1

51–9 51–8 51–7 51–6 51–5 51–4 51–3 51–2

52–9 52–8 52–7 52–6 52–5 52–4 52–3

53–9 53–8 53–7 53–6 53–5 53–4

54–9 54–8 54–7 54–6 54–5

55–9 55–8 55–7 55–6

56–9 56–8 56–7

57–9 57–8

58–9

Переход через 100

+100

91+9

92+9 92+8

93+9 93+8 93+7

94+9 94+8 94+7 94+6

95+9 95+8 95+7 95+6 95+5

96+9 96+8 96+7 96+6 96+5 96+4

97+9 97+8 97+7 97+6 97+5 97+4 97+3

98+9 98+8 98+7 98+6 98+5 98+4 98+3 98+2

99+9 99+8 99+7 99+6 99+5 99+4 99+3 99+2 99+1

— 100

100–9 100–8 100–7 100–6 100–5 100–4 100–3 100–2 100–1

101–9 101–8 101–7 101–6 101–5 101–4 101–3 101–2

102–9 102–8 102–7 102–6 102–5 102–4 102–3

103–9 103–8 103–7 103–6 103–5 103–4

104–9 104–8 104–7 104–6 104–5

105–9 105–8 105–7 105–6

106–9 106–8 106–7

107–9 107–8

108–9

История абакуса

Что такое абакус? Это древние счеты для вычислений. Ученые считают, что первый абакус появился в третьем тысячелетии до нашей эры в Месопотамии. Сейчас на её территории находится Ирак, Сирия и части Турции и Ирана. В 5 веке до нашей эры эти счеты узнали в Древнем Риме. Но это лишь предположения. Зато есть четкие доказательства того, что в 17 веке абакус точно был в Европе: в Парижской национальной библиотеке до сих пор хранятся сами счеты абакус и его схема.

В китайских национальных книгах 2 века нашей эры говорится о счетах суаньпань. Это аналог абакуса. Именно в этой стране счёты усовершенствовали, а потом отправили в Японию. Жители страны восходящего солнца убрали одну косточку и назвали счёты по-своему – соробан. Это значит «доска для вычислений». Счёты были очень популярны, потому что тогда в Японии торговля переживала свой расцвет, и знания математики были очень нужны.

Этимология

Латинское слово abacus произошло от греческого ἄβαξ (абакс), что означает что-то без основы и неправильно, либо кусочек прямоугольной доски или планка. В качестве альтернативы, без ссылки на древние тексты по этимологии, было высказано предположение, что это означает «квадратная табличка, усыпанная пылью», или «доска для рисования, покрытая пылью (для использования в математике)» (точная форма латыни, возможно, отражает родительную форму греческого слова, ἄβακoς абакос)

Принимая во внимание, что «табличка, усыпанная пылью» популярна, есть те, которые не доверяют этому предположению вообще и фактически утверждают, что это не доказано. Сам греческий ἄβαξ, вероятно, является заимствованием из северо-западного семитского языка, возможно, финикийского, и ассоциируется с еврейским словом bābāq (אב) или «пыль» (в пост-библейском смысле означает «песок, используемый в качестве пишущего поверхности»).

Школа ментальной арифметики AMAKids

«Академия развития интеллекта AMAKids» рада принять детей от 5 до 16 лет, чтобы научить их ментальной арифметике. Наша компания имеет Лицензию Департамента Образования, а разработки, методические материалы и учебники одобрены экспертами Роскомнадзора. Более 800 центров уже работают в 14 странах мира.

Ученики AMAKids занимаются в группах по максимум 10 человек. Это позволяет найти к каждому ребенку индивидуальный подход. Группы сформированы по возрастному признаку: младшая (5-6 лет), средняя (7-10 лет) и старшая (11-16 лет). Занятия проходят в два урока по 35 или 45 минут в зависимости от возраста детей.

Несмотря на то, что тренировка в «Академии развития интеллекта AMAKids» проходит раз в неделю, заниматься дома нужно ежедневно. Для этого наши специалисты создали уникальную онлайн-платформу, на которой можно выполнять домашнее задание, смотреть расписание, соревноваться с другими учениками и участвовать в олимпиадах.

Ментальная арифметика от AMAKids — это основа для успешной подготовки и учебы в школе, а также уверенность в будущем вашего ребенка!

Инструкция по применению

Сегодня вовсе не обязательно посещать специальную школу для изучения устного счета на абакусе. Вместо этого можно попробовать онлайн-тренажеры с разными уровнями, предназначенные не только для начинающих, но и для продвинутых счетоводов.

Положение пальцев и простые примеры

Вне зависимости от степени сложности выбранного задания, определяющее значение будет иметь положение пальцев, для чего была разработана специальная техника, облегчающая счет. Так, в случае применения японского абакуса необходимо задействовать только два пальца: указательный и большой. Согласно старинным схемам, большой палец предназначается для того, чтобы править костяшками из нижней палубы, тогда как указательный годится для всех бусин без исключения.

Кроме того, важную роль в этом вопросе играет и характер выполняемой счетной операции, ведь если, к примеру, речь идет о вычитании шариков земного ряда, то лучше всего делать его с помощью указательного пальца при прибавлении большим. В то же время для управления костяшками из небесной планки специалисты советуют ограничиваться одним только указательным пальцем, невзирая на то, что нужно сделать — прибавить или отнять.

Разобравшись с положением пальцев и кистей в целом, можно приступать к вычислению, начиная с установки счетов на горизонтальную поверхность и перевода всех их бусин в нулевое положение. Далее можно привести несколько элементарных примеров, как считать на абакусе, выполнив сложение следующих чисел:

«1+3». Чтобы сложить эти простейшие числа, необходимо перевести одну костяшку из земного ряда в сторону разделительной планки, а потом добавить к ней еще три бусинки, получив значение «4».
Выполнение вычисления до пяти предполагает перенесение одной бусины в сторону разделительной планки с одновременным перемещением всех остальных костяшек в нижнее положение.
Для получения числа «7» следует добавить еще две костяшки к разделительной планке, получив один небесный шарик, соответствующий пяти, и два земных, равных двум (5+2=7).

Сложение/вычитание и умножение/деление

Набив руку в наборе однозначных и многозначных чисел и научившись прибавлять и отнимать самые простые из них, можно смело переходить на следующий, более сложный уровень. И прежде всего речь идет о сложении и вычитании двухзначных чисел. К примеру, посчитать, сколько будет 27+43, на абакусе можно будет следующим образом:

Прежде всего на счетах набираются оба числа с обязательным разложением их на простые составляющие (7 и 3 к единицам, 2 и 4 к десяткам).
После этого выполняется простейшее попарное сложение цифр — 2+4 и 7+3.
Из-за того что при сложении единиц получается 10, необходимо привести все костяшки в этом ряду в нулевое положение, добавив единицу к ряду десяток, получив в итоге 30.
Так как добавляются не только единицы, но и десятки, то к полученным 30 необходимо прибавить еще 4, в результате чего должно остаться 7 десятков, разложенных на одну небесную пятерку и 2 земные единички из ряда десятых.

Вычитание выполняется на основе аналогичного алгоритма, но только в обратную сторону, предполагающую отнимание десятых и добавление единиц, если таковые будут образовываться в остатке. Что касается умножения, то с ним также не должно возникнуть никаких трудностей, нужно только освоить таблицу умножения от 0 до 10.

Само решение выполняется в два этапа, которые предполагают разложение каждого числа на десятки и единицы с последующим их перемножением. Если же для расчета используются трехзначные и более сложные числа, следует придерживаться одного простого правила, согласно которому сначала перемножаются десятки, потом единицы с десятками и наоборот, а после сами единицы. Проще говоря, счет ведется от большего к меньшему с последовательным их набором на абакусе. По аналогии выполняется и деление, главное, не сбиться и соблюдать очередность выполняемых операций.

Предыдущая
МатематикаУмножение и деление — примеры решения задач по математике для 3 класса
Следующая
МатематикаСвойства сложения — основные законы, формулы и правила

Дополнительная литература

В общем, примерно вот по такой схеме на абакусе и считают. Я показала все самое простое. А ведь можно еще и вычитать, и умножать, и делить, и в степень возводить. И работать с огромными числами. Хотите знать больше? Пожалуйста! Обнаружила в интернете инструкцию по работе с соробаном. Вот здесь ее можно скачать.

Если не поможет инструкция, то может быть стоит обратить внимание на книгу «Ментальная арифметика. Знакомство»? Насколько я поняла, она ориентирована на обучение детишек

Такой своеобразный учебник. Нашла я ее в магазине «My-shop». Ссылка на эту книжку чуть ниже.

Ментальная арифметика. Знакомство — Багаутдинов Р. | Купить книгу с доставкой | My-shop.ru

Думаю, что и взрослым людям не повредят занятия с абакусом. Особенно бухгалтерам. Представляете, все коллеги на калькуляторах считают или на компьютерах. А вы такой деловой с абакусом) И батарейки-то не садятся, и кнопки не западают, и костяшки так приятно пощелкивают) Красота!

Уф, наверное, хватит на сегодня счета. Теперь давайте посмотрим, как другие считают. Настоящие маленькие абакус-мастера, только они уже на том уровне подготовки, когда хватает и воображаемых счет. Смотрим видео.

На сегодня, пожалуй, все. А завтра на блоге «ШколаЛа» вас ждет новая интересная информация!

Кстати, если есть желание каждое воскресение по почте получать анонсы статей на следующую неделю, то обязательно подпишитесь на новости блога. Тогда вы точно ничего не пропустите!

И не забудьте вступить в нашу группу «ВКонтакте», там вас тоже ждет много всего интересного!

Удачи вам и вашим маленьким школьникам!

Евгения Климкович.

Преимущества использования абакуса и обучения ментальной арифметике

Косточки абакуса, продающегося в наше время, имеют острые концы.  Во время обучения улучшается мелкая моторика рук. На первом занятии ученики сначала узнают, как правильно поставить руки. Чтобы урок не стал скучным, тренер регулярно проводит небольшие игры.

Чем раньше начинаются уроки по данной программе, тем лучше будет переход от использования настоящих счётов к ментальным. Специалисты считают, что лучшее время для этого 5-6 лет. В данный период у детей хорошо развивается фантазия и воображение, они начинают интересоваться учёбой. Постоянные уроки по данному курсу повысят у вашего сына или дочери отметки по всем учебным дисциплинам, а также сформируют у него правильное представление об обучении.

Благодаря ментальной арифметике у ребенка:

• улучшается память и воображение;
• развивается образное мышление;
• формируется усидчивость, сосредоточенность и концентрация внимания;
• возникают лидерские качества;
• развиваются аналитические и творческие способности;
• одновременно работают два полушария мозга.

Основной плюс древних счётов в том, что ребёнок не просто учит конкретные задачи, а запоминает числа в форме изображений. Это мотивирует воображение. Мгновенный устный счёт – отличное дополнение к итогам обучения ментальной арифметике.

Что такое абакус?

Вот она – эта загадочная счетная машинка.

Чем-то напоминает известные многим советские счеты с костяшками. И, насколько я поняла, принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками.

Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре.

Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки.

Плюсы ментальной математики:

• развиваются математические способности;
• улучшается память;
• усиливается концентрация внимания;
• появляются нацеленность на успех и умение нестандартно мыслить и находить решение в условиях многозадачности;
• развиваются образное мышление, логика;
• растет тяга к новым знаниям и умениям.
  Всего не перечислить.

К минусу можно отнести стоимость обучения по этой методике. Весь волшебный математический фейерверк, в который входят не только счет на счетах, но и прочие сопутствующие занятия — возможно, даже и танцы с пением да стихами (зависит от конкретных курсов), выливается в кругленькую сумму.

Работа с родителями в Ментальной Арифметике

Нельзя показывать родителям формулы, двузначные/трехзначные примеры, умножение/деление на соробане, потому что это отбивает интерес к ментальной арифметике. После этого родители уже не будут так увлеченно слушать преподавателя.

Что такое ментальная арифметика?

Польза ментальной арифметики.

Японская методика. Япония — одна из самых развитых стран.

Возраст. Три категории возрастов.

Уровни. 10 уровней по 3,5 месяца.

Школьная методика и ментальная арифметика.

Результаты через год/два года/три года занятий ментальной арифметики.

Необходимо ежедневное выполнение домашнего задания — сообщить это нужно на пробном уроке, чтобы в будущем не было возмущений.

Результат будет только если родители ежедневно быстро диктуют примеры, а ребенок решает на соробане и затем ментально.

Стоимость курса, учебников — данную информацию нужно сообщать в конце презентации. Если сообщить вначале, то дальше преподавателя слушать не будут, главное родители уже услышали.

Провести работу с родителями нужно провести так, чтобы не оставалось вопросов.

Ответы на вопросы родителей. Раздаем лист для записи контактных данных учеников (смена, возраст, фио, тел и т.д.).

Образец скрипта проведения пробного урока

«Добрый день, уважаемые родители и ученики! Моё имя… я преподаватель/представитель центра по ментальной арифметике.

Наверняка большинство из вас уже слышали о ментальной арифметике, сегодня расскажу вам более подробно информацию, затем мы порешаем примеры на соробане с ребятами и все желающие смогут записаться.

Ментальная арифметика появилось более 2000 лет назад в древней Азии, получила широкое распространение в Японии, а теперь дошла до нашей страны. Главный инструмент в ментальной арифметике это соробан.

Соробан состоит из деревянной рамы, спиц, и нанизанных на них косточек. Древние китайцы верили, что верхние косточки ассоциируют небо, а нижние землю, линия ответа — горизонт.

Далее демонстрируем как считать, только прямое сложение и вычитание, то есть без формул. Например, 1+1+2, 2+2—1, 3+1—4 и т. д.

Сейчас мы давайте посчитать на соробане с ребятами.

По 2–3 ребенка приглашаем к демонстрационному соробану и диктуем несколько легких примеров в 3–4 ряда (прямой счет без формул). Создаем атмосферу соревнования.

Как только все дети попробовали решить примеры на соробане, убедились что это легко и весело, зарядились эстафетой, проводим ментальный счет для детей и родителей. Все вместе «хором» решают примеры под диктовку.

Ментальная арифметика развивает:

— Скорость мышления

— Память

— Внимательность

— Усидчивость

— Фотографическую память

— Творческое аналитическое мышление

— Логику

— Творчество

— Слуховую память

— Мелкую моторику рук при работе на соробане, что способствует развитию интеллекта.

Существуют три возрастные категории: дошкольники (4–6), школьники (6–8) и старшая группа (9–16). Вышеперечисленные возрастные категории проходят курс обучения за разный период времени, в зависимости от успеваемости группы. Каждый уровень обучения в среднем занимает от 2 до 4 месяцев, кроме детей в возрасте 4–5 лет, у них изучение 1 уровня может занимать до 6 месяцев.

Полный курс ментальной арифметики состоит из 10 уровней, которые включают в себя основные блоки: сложение и вычитание, умножение и деление, возведение в степень и извлечение из под корня. Затем с каждым уровнем увеличивается разрядность чисел.

Главная цель ментальной арифметики —это развитие мозговой активности у детей. Этому результату способствует одновременное развитие двух полушарий головного мозга. Левое полушарие отвечает за логику, а правое за творчество. Во время ментального счета ребенок представляет перед собой абакус, то в это время работает правое полушарие, а когда начинает считать на воображаемом абакусе, то начинает работать логика — левое полушарие. В итоге, во время ментального счета работают одновременно оба полушария мозга.

Ученикам становится легче усваивать новый материал, повышается успеваемость по школьным предметам, вырабатывается внимательность.

Уроки будут проводится 1 раз в неделю по 2 часа, для всех возрастов, кроме 4–5 летних учеников, для них занятия проводятся 2 раза в неделю по 50 минут.

Стоимость обучения за 4 занятия составляет ______.

Уважаемые родители, если есть вопросы, будем рады ответить на них.

Итак, мы раздадим вам анкеты, которые вы можете заполнить чтобы записаться на обучение”.

Как складывать и вычитать?

После того как малыш научился выкладывать числа, можно приступать к обучению простейшим арифметическим действиям.

Сначала рассмотрим сложение, к примеру, 36+23:

1. Устанавливается первое число, 36.
2. Далее его следует разделить на простые цифры – 3 и 6.
3. После этого на соответствующих линейках провести сложение единиц с единицами, десятков и десятками. Получается: 3+2 (десятки) и 6+3 (единиц).
4. Кости на линейках перемещаются соответствующим образом.

Если бы косточек получилось больше 9, нужно было прибавить единицу на соседней линейке.

Вычитание проводится по такой же системе, начиная с меньшего порядка. В случае, если из меньшего числа вычитается большее, происходит следующее: их переставляют, а на соседней линейке убирают косточку.

Такая система счета кажется сложной только при описании, на деле же стоит попробовать – и ребенку непременно понравится.