Вычитаем столбиком с примерами на картинках

Второй пример вычитания столбиком

Первый пример был очень простым, потому, что все цифры второго числа были меньше чем верхние…

Давайте возьмем другое число и попытаемся отнять столбиком…

Нам потребуется занимать десятки…

Давайте отнимем от 8345 число 978.

Первый пример был очень простым, потому, что все цифры второго числа были меньше чем верхние…

Давайте возьмем другое число и попытаемся отнять столбиком…

Нам потребуется занимать десятки…

Давайте отнимем от 8345 число 978.

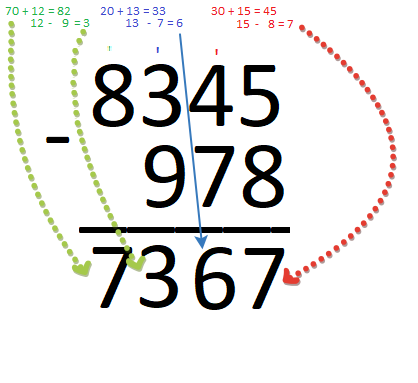
Опять выграниваем по правому краю.

Здесь существует правило! Если в одном столбце верхняя цифра меньше нижней, то нужно занимать единицу у следующей слева цифры.

Красным цветом…

Отнять от 5 8 не получится. Поэтому нужно занять единицу от 4 ставим апостроф над цифрой 4 – это означает, что там уже не 4, а на единицу меньше… 3

Чтобы понять, что это значит, то возьмите число 45 и представьте ё в виде 45 = 30 + 15

30 – это первая цифра(3) этого числа = 4 с апострофом и от 15 вычитаем 8 = 7 – опускаем за черту…

Синим цветом

4 с апострофом = 3 от неё надо вычесть 7 – повторятся аналогичная ситуация, что и первом случае…

Ставим апостроф над 3 , забираем оттуда десяток, у нас получилось 13 – 7 = 8 – опускаем за черту…

Зеленым цветом

Вместо 83 у нас 82, можно отнять так же столбиком, а можно и так… в уме 82 – 9 = 73

Опять выграниваем по правому краю.

Здесь существует правило! Если в одном столбце верхняя цифра меньше нижней, то нужно занимать единицу у следующей слева цифры.

Красным цветом…

Отнять от 5 8 не получится. Поэтому нужно занять единицу от 4 ставим апостроф над цифрой 4 – это означает, что там уже не 4, а на единицу меньше… 3

Чтобы понять, что это значит, то возьмите число 45 и представьте ё в виде 45 = 30 + 15

30 – это первая цифра(3) этого числа = 4 с апострофом и от 15 вычитаем 8 = 7 – опускаем за черту…

Синим цветом

4 с апострофом = 3 от неё надо вычесть 7 – повторятся аналогичная ситуация, что и первом случае…

Ставим апостроф над 3 , забираем оттуда десяток, у нас получилось 13 – 7 = 8 – опускаем за черту…

Зеленым цветом

Вместо 83 у нас 82, можно отнять так же столбиком, а можно и так… в уме 82 – 9 = 73

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями:

Как вычитать столбиком

Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков – десятки и т. д. Результат вычитания записывают под чертой:

Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:

От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:

В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:

Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:

При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 – получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 .

Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:

Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:

Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:

В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:

Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:

А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:

Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.

Как записывать деление в столбик

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Методика обучения делению в столбик

Чтобы приступить к этому арифметическому действию, нужно познакомить ребенка с названием элементов при делении.

Делимое – число, что подвергается делению, делится на делитель, в результате получается частное.

Объясняют ему саму суть операции деления столбиком. Это такое действие в математике, которое применяют для разделения чисел за счет дробления самого процесса деления на более простые шаги.

Деление в столбик на конкретном примере

Метод деления, основанный на конкретном примере, очень распространен и используется школьниками в дальнейшей учебе. Ребенку предлагается разделить число 945 на 5 в столбик.

Шаг 1. На этом этапе нужно попросить ребенка показать компоненты деления. Если он правильно усвоил выше изложенный материал, то без особых усилий определит: 945 – это делимое, 5 – делитель, результат деления – частное. Собственно, это то, что и необходимо найти.

Шаг 2. Сначала ребенка просят записать рядом 945 и 5, а потом делят их «уголком».

Шаг 3. Следующий этап, просят ребенка рассмотреть делимое и, продвигаясь вправо, предлагают определить самое меньшее число, что больше делителя. Ученик определяет числа: 9, 94 и 945. Самым меньшим из них является 9. Потом спрашивают, сколько раз 5 помещается в числе 9? Ребенок дает ответ, что один раз. Значит, пишут 1 под чертой – первую цифру искомого частного.

Вот и столбик скоро получится.

Шаг 4. На следующем этапе предлагают ребенку умножить 1 на 5 и получают 5. Просят записать результат, который получили, под первой цифрой делимого, и из 9 вычитают 5. Спрашивают ребенка о результате и получают 4.

Здесь важно объяснить ему, что результат вычитания всегда будет меньше делителя. А когда наоборот, значит, неправильно удалось определить, сколько раз 5 содержится в 9

Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого. Ребенок определяет 4 и пишет к четверке.

Шаг 5. Дальше задают ему знакомый вопрос о том, сколько раз 5 помещается в 44? Ученик отвечает, что восемь раз. Тогда предлагают записать восьмерку к единице под чертой. Объясняют ребенку, что это будет следующая цифра искомого частного. Просят умножить 5 на 8. Получается 40, и записывают эту цифру под 44.

Шаг 6. На следующем этапе вся операция повторяется. Ученик вычитает 40 из 44, и получает 4 (4 меньше 5, значит, ребенок все делает правильно). Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.

Снова задают тот же вопрос. Сколько раз 5 помещается в 45? Ребенок отвечает, что девять раз.

Шаг 7. Просят его записать девятку под чертой. Предлагают умножить 5 на 9. Ребенок говорит, что получает в результате 45 и записывает в столбик под 45. Дальше проводит вычитание 45 из 45, и получает 0. Ему объясняют, что это был пример деления числа без остатка.

Когда ребенок неплохо умеет пользоваться таблицей умножения, деление в столбик для него простой задачей

Очень важно с помощью постоянных примеров и упражнений закрепить полученный навык

Вычитание столбиком из чисел, содержащих нули.

Опять же, разберем на примере:

Записываем числа в столбик. Которое больше — сверху. Начинаем вычитание справа налево по одной цифре. 9 — 3 = 6.

Из нуля вычесть 2 не получится, тогда опять занимаем у цифры слева. Это нуль. Ставим над нулем точку. И снова, у нуля занять не получится, тогда двигаемся дальше к следующей цифре. Занимаем у единицы. Ставим над ней точку.

Обратите внимание: когда в вычитании столбиком над 0 есть точка, нуль становится девяткой. Над нашим нулем есть точка, значит, он стал девяткой

Вычитаем из нее 4. 9 — 4 = 5. Над единицей есть точка, то есть она уменьшается на 1. 1 — 1 = 0. Полученный нуль не нужно записывать

Над нашим нулем есть точка, значит, он стал девяткой. Вычитаем из нее 4. 9 — 4 = 5. Над единицей есть точка, то есть она уменьшается на 1. 1 — 1 = 0. Полученный нуль не нужно записывать.

Учимся решать примеры в пределах 10

Теперь пора переходить к тому, как научить ребёнка считать примеры. Главное правило — практические действия и многократные тренировки. В идеале ребенок должен запомнить результаты всех примеров в пределах 20. Однако добиться этого путем механического заучивания очень сложно. Лучше делать это на основе выполнения различных интересных упражнений. Работая над их решением, ребенок постепенно запомнит все ответы в примерах. Приведем описание таких игр.

Таблица до 10

Очень эффективно использование карточки — таблицы. Она разделена на два ряда по пять ячеек в каждом. Также к этой карточке прилагаются 10 фишек. Ребенок в ячейки выкладывает нужное количество фишек, затем добавляет или убирает несколько и подсчитывает результат.

С помощью такой таблицы можно не только решать примеры. У ребенка постепенно откладывается в памяти зрительный образ каждого числа и в дальнейшем это очень поможет делать уже подсчеты в уме.

Счет на пальцах

Традиционно ребенку часто предлагается считать примеры с использованием пальцев. Это очень удобно, поскольку данный способ можно применять в любой ситуации. Поэтому некоторые специалисты категорически против обучения детей счету на пальцах. Они утверждают, что после этого будет трудно  научить ребенка считать примеры в уме, ведь он продолжит подсчеты «по-старому». Практика показывает, что это не так. Дети с легкостью переходят на устные вычисления, как только у них это будет получаться быстрее, чем «вручную».

Счеты

Также популярным является обучение решать примеры на счетах. С помощью этого приема у ребенка тоже формируется зрительный образ числа, что поможет делать подсчеты в уме.

Ручной калькулятор

Можно вместе с ребенком сделать самодельный калькулятор. Для этого понадобиться картонная коробка и два одноразовых стакана. У стаканов надо отрезать низ  и прикрепить их на боковую стенку коробки так, чтобы они не доставали до ее дна. Между стаканами на стенке написать знак «+», а внизу знак «=».

Чтобы посчитать пример ребенок в первый стаканчик бросает столько бусинок (макарон, пуговиц и т.п.), как показывает первое число, а во второй — как второе число.  После этого подсчитывает общее число бусинок, оказавшихся в коробке.

Прищепки

Для формирования вычислительных навыков можно использовать прищепки. В качестве основы можно изготовить любые картонные шаблоны (солнышко, цветок, смайлик, личико и т.п.). Ребенок будет решать примеры, прикрепляя и убирая прищепки. Это занятие для него интереснее, чем простое использование счетного материала.

Линейка

Для развития у ребенка умения делать вычисления многие учителя используют линейку. Сначала на линейке нужно найти первое число из примера, а затем переместиться на нужное количество делений вправо (если «+») или влево («-»). Число, на котором остановились и есть ответ в примере.

Такой способ основывается на знании числового ряда. Он демонстрируется во многих учебниках по математике для 1 класса. С его помощью можно легко объяснить, как нужно прибавлять и вычитать числа 1, 2, 3 и 4 путем перехода или перепрыгивания через числа. 

Интерактивные игры и тренажеры

Интерактивные игры с генерацией звуковых фраз «Игротека Гнома»

Тренажёр по математике «Устный счёт в пределах 10 и состав числа»; 1 класс.

Тренажёр по математике «Царевна-лягушка. Счёт в пределах 10»; 1 класс.

А также  другие презентации и материалы по теме:

• Интерактивные тренажеры на сложение и вычитание.
• Счет в пределах 10, счет в пределах 20, тренажеры на устный счет и еще множество других материалов на сайте.

Делим столбиком – приведем пример

Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.

Объясняем наглядно

Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.

Шаг 1
. Записываем числа, разделив их «уголком».

Шаг 2.
Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.

Шаг 3.
Переходим к оформлению деления столбиком:

Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.

Записываем результат.

Шаг 4.
Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.

Шаг 5.
Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.

Шаг.6
Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.

Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.

Шаг.7
Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.

Деление в столбик – правила

Для того, чтобы уметь делить в столбик необходимо знать некоторые правила. Именно об этом и пойдет далее речь. Ведь деление в столбик невозможно освоить если не знать элементарного – таблицы умножения. Считать простые примеры на умножение необходимо быстро и в уме. Это только в начале обычно дети пользуются черновиками, чтобы подобрать множитель, таким образом найти частное. Еще надобно уметь разбивать числа на сотни, десятки, тысячи – не путаться и в этих понятиях. Для наглядности, где делимое, где делитель, где частное можете изучить термины на изображении ниже.

Что нужно знать для деления в столбик?

Прежде, чем приступать к делению, следует проверить ребенка на знания элементарных правил. Ведь пропускать математику нельзя. А если пропуски все же были, то нужно изучить тот материал, что изучали ранее на уроках в школе

Понадобится обратить внимание на такие знания, как:

Запомнил ли школьник, как называются все элементы, участвующие в процессе деления.

Обратите внимание на знание таблицы умножения ребенком.
Еще ребенок должен усвоить, какие бывают разряды числа (единицы, десятки, сотни).

Пример: 

1. 57: 3, где 57 – это делимое, число, что разделяют на доли, а 3 – это делитель, указывающий, на сколько делить предыдущее число.
2. Определяемся, вначале какие единицы выделить в делимом для осуществления деления в столбик числа 57. Число 5 > 3.
3. Узнайте, сколько раз следует взять число 3, чтобы получить 5. Результат 3 · 1 = 3 ≤ 5. Значит подходит и 1 поставьте в качестве первой цифры частного.
4. Теперь вычитание: 5 — 3 = 2. Остаток 2 и единицу сносим, выходит 27.
5. Находим теперь, на какое число нужно умножить 3, чтобы результат был 27. Согласно таблице умножения 3 · 9 = 27.
6. Итого результат 19.

Умножение, деление – взаимосвязаны между собой, хотя и противоположные операции. Чтобы проверить, верно ли нашли частное, необходимо выполнить умножение. Потому таблица умножения и умение умножать на черновике без калькулятора всегда пригодится ребенку, также еще при умножении следует уметь правильно прибавлять, а при делении в столбик вычитать. В математики все действия с числами между собой взаимосвязаны.

Ниже смотрите пример деления в столбик 536 на 4. Действия с трехзначным делимым выполняются аналогично, что и с двухзначным.

Деление

Деление в школе начинают учить уже с третьего класса. Школьники только изучают азы процесса, выполняют самые простые примеры на это действие.

Примеры подобны умножению, только детей учат таблице деления, а не умножения. Школьники должны уловить саму суть, что означает поделить число на несколько частей, изучают, что такое делимое, делитель, частное. Узнают, как проверить умножением правильность решения примера или же задачи. В столбик дети еще не считают, так как даются самые простые примеры и все числа из таблицы умножения. Пример: 81 : 9 = 9.

Процесс деления в четвертом классе значительно усложняется. Детям дают вначале года вспомнить, что они учили в третьем классе, а далее уже начинают осваивать технику деления чисел в столбик. Именно за этот учебный год осваивают такие знания. Ниже приведен алгоритм решения примеров в столбик с подробным описанием процесса.

Здесь даже учтено то, что возможно будет остаток при делении, что число получится не цельным, а через запятую.

Деление в столбик – примеры для тренировки

Без множества примеров трудно освоить технику деления в столбик. Можно перерешать кучу примеров и тогда в любом случае материал усвоится хорошо. Ниже представлен пример деления числа 748 на 2. Давайте разберем этот простой пример деления в столбик.

1. У делимого следует выделить сотни, точнее их 7 у делимого. Для этой цифры подбираем множитель: 2 · 3 = 6 ≤ 7, значит подходит.
2. Пишем 6 под семеркой, а 3 под чертой, это одна из цифр частного.
3. Вычтем из 7 — 6 = 1, и сносим 4. Теперь подбираем множитель: 2 · 7 = 14 = 14 — результат верен. Вторая цифра частного 7.
4. Пишем 14 под 14, и сносим следующую цифру делимого 8. Подбираем множитель: 2 · 4 = 8 = 8, разница 0, число делится без остатка.
5. Итак, результат 374.

Пример деления

Этот пример решен, существует и множество других примеров, которые будут представлены далее по тексту на фото. Эти примеры – готовое решение домашних задач, где подробно расписан процесс деления в столбик, как находится каждая цифра частного. Когда все их перерешаете самостоятельно, то дело доведется до автоматизма и вы сможете решить задание любой сложности, пользуясь своим умением.

Делить в столбик, пожалуй, одна из самых непростых тем в математики. Как уже упоминалось, в процессе используют все четыре действия, (начиная от сложения, заканчивая умножением). Без знаний этих процессов никак не обойтись. Некоторые думают, что зачем знать, как делить, если есть калькуляторы. Но не всегда бывают они под рукой, а посчитать надо сдачи или другую величину, и знания пригодятся на практике. Далее изучите примеры на эту тему.

Пример деленияалгоритмы деления в столбикДеление трехзначного и четырехзначного числаДеление 693 на 3Деление чисел с нулямиДеление без остатка

Еще здесь на портале вы можете узнать много интересного на тему образования вот в этих текстах:

1. Сказка «Репка» по ролям в школе;
2. Сочинение по басне Крылова «Ворона и лисица»;
3. Сочинение на тему «Моя будущая профессия»;
4. Считалки для детей разного возраста;
5. Как правильно писать – на здоровье?

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий. Например, возьмите числа 196 и 28 и объясните принцип:

1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.
2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.
3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370

Важно начинать запись с первого числа слева.

После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74

Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка. 4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.